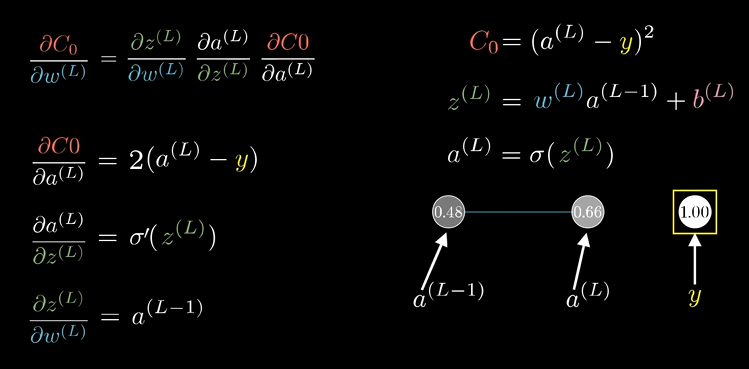神经网络的结构
视频教程:
【官方双语】深度学习之神经网络的结构 Part 1 ver 2.0
【官方双语】深度学习之梯度下降法 Part 2 ver 0.9 beta
【官方双语】深度学习之反向传播算法 上/下 Part 3 ver 0.9 beta
神经网络结构
神经网络的变种有很多:
- 卷积神经网络 Convolutional neural network 擅长图像识别 image recognition
- 长短期记忆网络 Long short-term memory network 擅长语音识别
- 多层感知器 MLP(Multilayer Perceptron) 经典原版,就是下面的结构
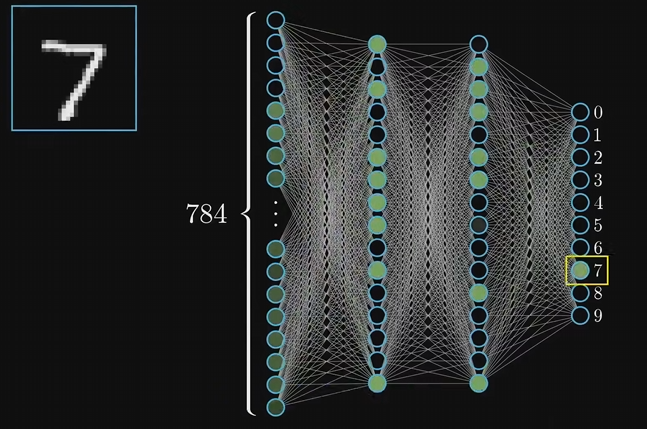
神经网络名字来源于人类大脑,神经元是什么又是如何连接的。
神经元看作一个装有数字的容器,一般是0到1区间,上面的结构把图片的每个像素都输入到网络对应的神经元中,值为像素的灰度值,值越大像素越白。
一般把神经元中装的值叫做 激活值 Activation
网络中最后一层的十个神经元代表0到9十个数字,他们的激活值也在0到1之间,激活值表示系统认为输入的图像对应着哪个数字的可能性。
网络中间还有几层 隐含层 Hidden layers,例子中选择了两层隐含层,每层16个神经元,随便选的
神经网络运作时,上一层的激活值将决定下一层的激活值,所以神经处理信息的核心机制正是:一层的激活值是通过怎样的运算 算出下一层的激活值。可以看作是模仿生物中神经元组成的网络,某些神经元的触发,就会促使另一些神经元激发。

上层神经元如何影响下层神经元的激活值,给第二层的每个神经元与第一层所有神经元的每一条连线都附上一个权重值 Weights,这些权重都是数字而已
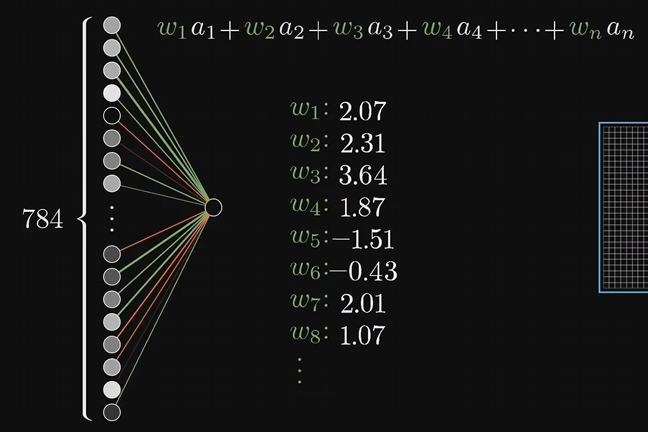
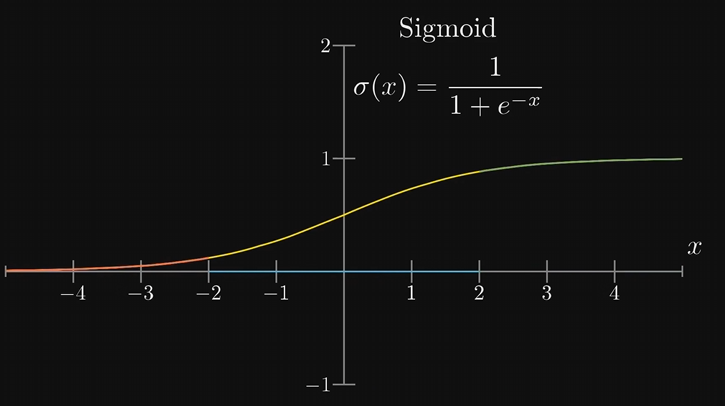
拿第一层的所有激活值,和每条边的权重一起,算出他们的加权和。这样算出来的值可能是任意大小,我们需要激活值都在0到1之间,可以通过某种函数来映射,比如:Sigmoid,这种函数一般叫激活函数Activation Function
所以激活值就是把上面算出来的加权值塞进sigmoid函数映射一下,但有时候即使加权和大于0,也不想把神经元点亮,比如规定加权和大于10的时候才激发,可以加上一个-10之类的数,叫做偏置 bias 。再将它送到sigmoid函数
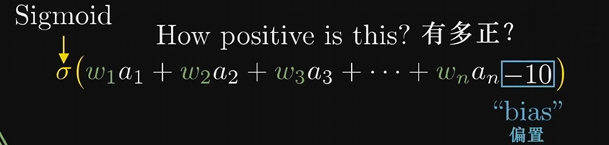
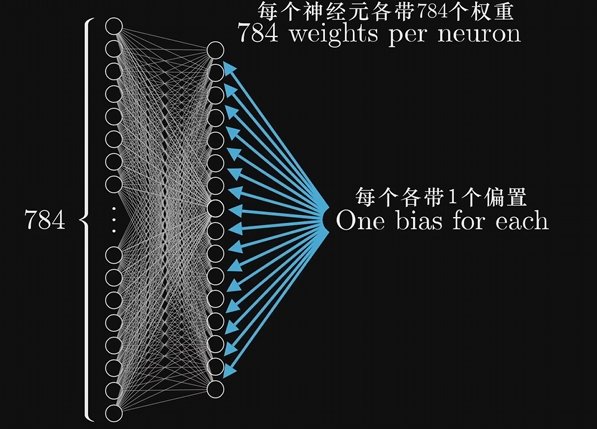
所有的权重和偏执都可以看作是旋钮开关供你调整,从而带来不一样的结果。学习或者说训练的过程,就是找到该如何设置这一坨参数,才能让它正确的解决问题。
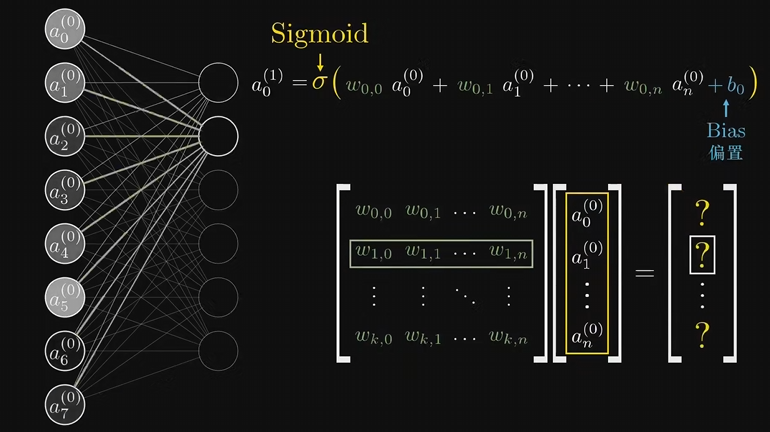
对于计算下层神经元的激活值,线性代数可以很方便表示
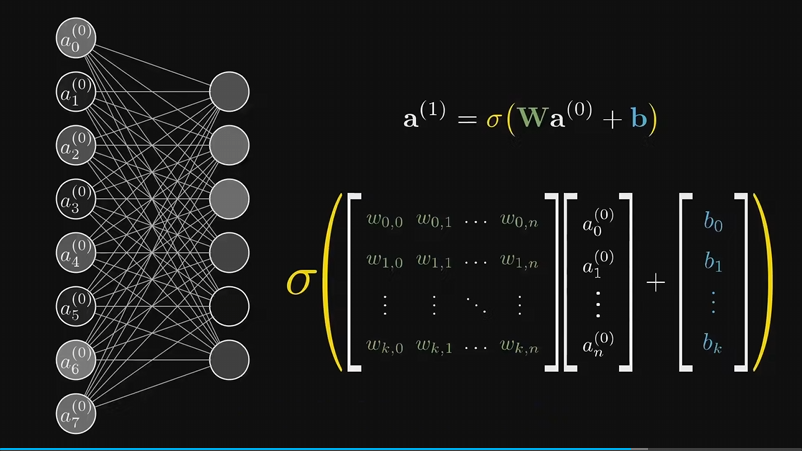
整个神经网络可以看作一个函数,例子是一个输入784个值,输出10个值的函数
梯度下降法
神经网络训练的过程,是不断调整权重和偏置这些参数,提高网络对训练数据的表现。最终我们希望这个网络可以举一反三,给它没见过的测试数据它也能正确处理。
在一开始,回完全随机的初始化所有的权重和偏置值,这个网络对于给定的训练示例,会表现的非常糟糕。
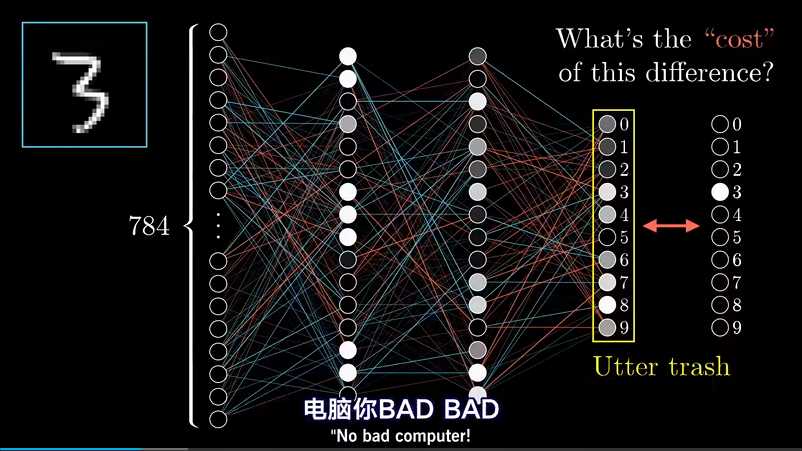
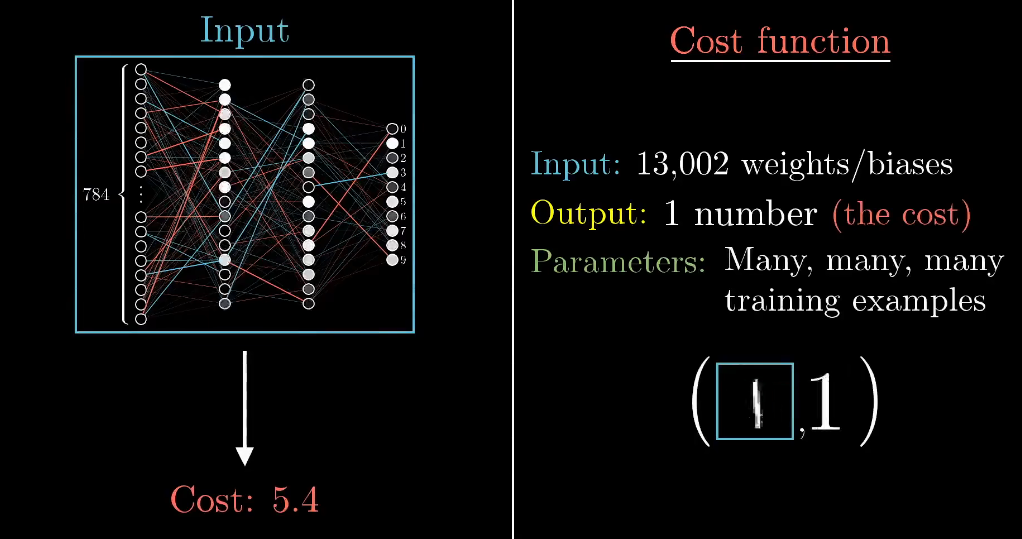
需要定义一个代价函数来告诉它,结果有多垃圾。

需要将每个垃圾输出激活值,与你想要值之间的差的平方和加起来。我们称之为单个样本上的代价(Cost 也可以叫 Loss),这个值越大,说明你的模型越找不到北。接下来要考虑所有训练样本中代价的平均值(这个值也叫 Empirical Risk 经验风险),用这个值来评价网络有多糟糕。
只告诉网络它有多糟糕是没啥用的,还得告诉他怎么改变这些权重和偏置值,才能有进步。
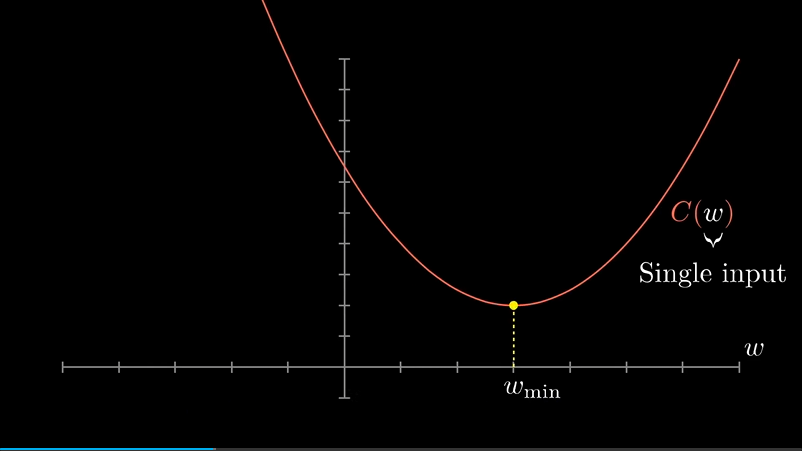
先不考虑13000个参数的函数,而先考虑简单的一元函数,怎么找到输入值x,使函数值最小化呢?
|
|
|---|
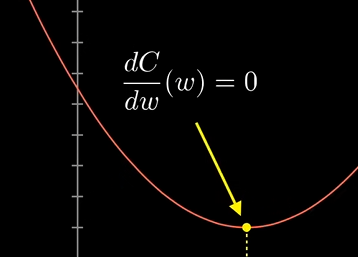
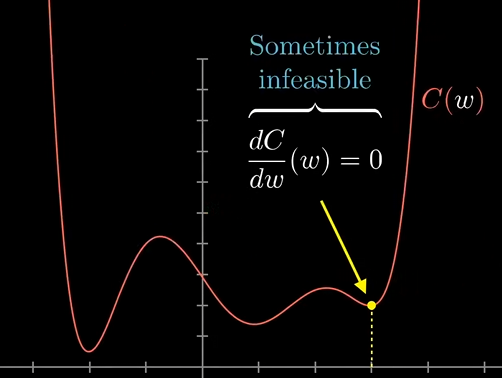
如果函数很简单,那么直接求斜率为0的位置就是答案,但如果函数很复杂,就不一定能写出来。对于13000个参数的网络,更加不可能。一个技巧是,先随便挑一个输入值,然后考虑向左走还是向右走,函数值才会变小。
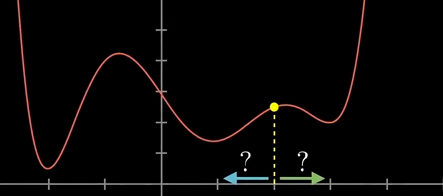
可以找到这个地方的斜率,如果为正0就往左走,为负就往右走,每次走一小步,不停的这样,就可以找到一个局部最小值。取决于一开始的输入,最后可能落到不同的坑里,可能并不是最优解,神经网络也会遇到这样的问题。
对于两个输入一个输出的二元函数,则可以看作为一个面,用同样的方法找到某个局部最深的坑
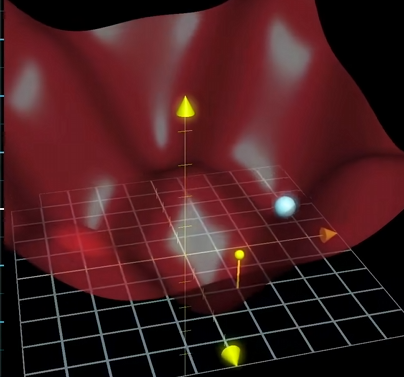
问题变成哪个方向下山最快。和一元函数的斜率一样,多元函数也有斜率,叫做梯度,梯度指出了函数的最陡增长方向。这种算法总结下就是:随便一个输入后,先计算梯度,再按梯度负方向走一小步下山,然后循环。处理13000个输入的函数也一样,这就是梯度下降算法
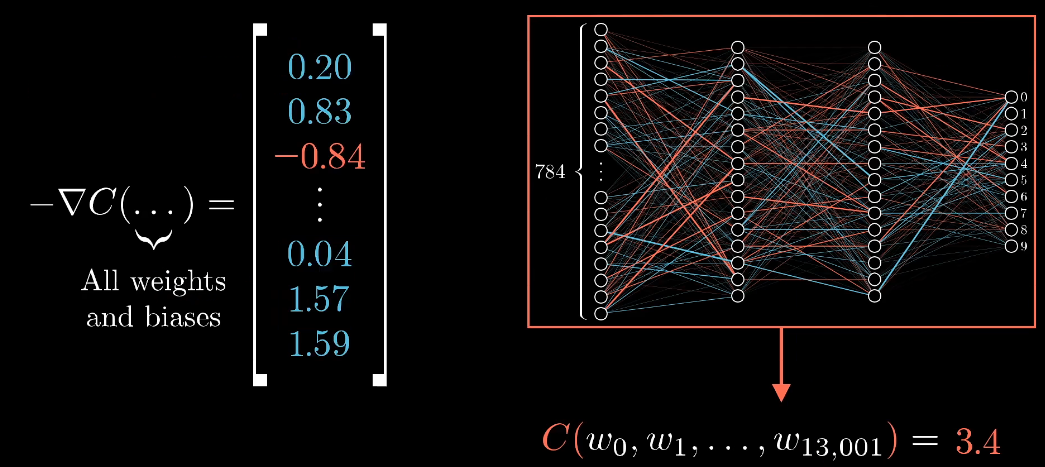
想象13000个输入的情况是很复杂的,不借助空间,把梯度看着一个向量,负梯度的每一项值都告诉我们两件事,正负号告诉我们输入向量的这一项应该调大还是调小,每一项值的相对大小告诉我们改变哪个输入影响更大。
在网络中,把13000多个权重和偏置作为输入,通过训练数据,得出一个对网络糟糕程度的评分。代价函数的梯度,告诉我们如何微调权重和偏置的值,才可以让代价函数改变的最快。
当你随机初始化权重和偏置,并通过梯度下降法调整了很多次参数之后,期望的是神经网络识别数字的正确率变高,包括识别从来没见过的图片。
反向传播
神经网络学习的核心算法。为了让整个网络的代价值越来越小,我们要求的是代价函数的负梯度,它告诉你如何改变所有权重和偏置,好让代价下降的最快。反向传播算法正是用来求这个复杂到爆炸的梯度的。
理论上因为代价函数牵扯到对成千上万个训练样本的代价取平均值,所以我们调整每一步梯度下降用的权重偏置,也会基于所有的训练样本。但为了计算效率,这里可以逃课,不必每一步都非得要计算所有的训练样本。
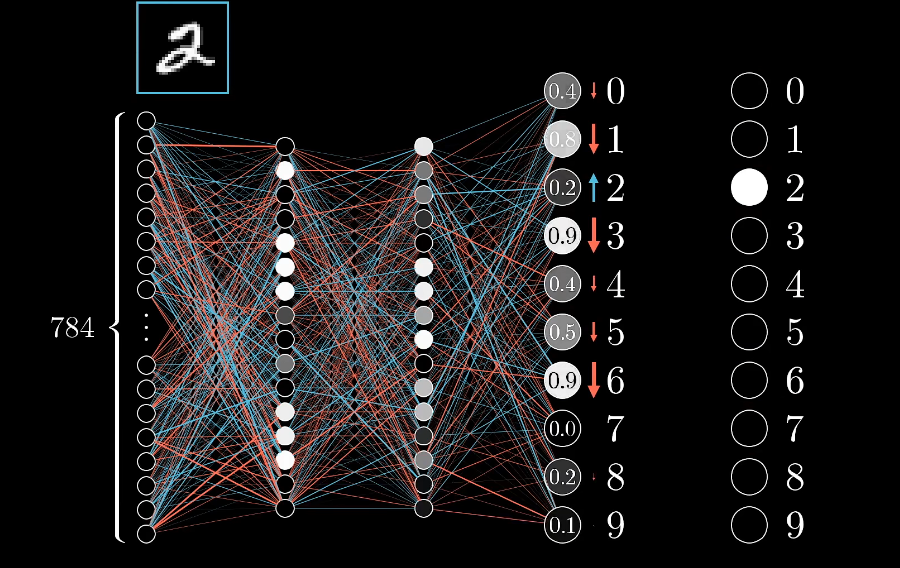
先只关注一个训练样本“2”,会对调整权重偏置产生什么影响,假设网络现在还没训练好,所以输出层的激活值看起来都很随机,我们希望输出结果时2,我们希望对于神经元的激活值变大,其余神经元的激活值变小。并且变动的大小应该与现在值和目标值之间的差成正比,比如增加2对应神经与的激活值,就比减少8的激活值更重要,因为8的激活值已经很接近目标了。

就先来关注一下2的神经元,它的激活值是上一层所有激活值的加权和 加上一个偏置,再通过sigmoid ReLu之类的激活函数算出来的。要增大这个激活值,有三条路:
- 增加偏置$b$
- 增加权重$w$
- 改变上一层的激活值$a$(注意不能直接改激活值,只能改上上层的权重偏置)
先看增加权重,各个权重的影响力是不同的,前一层的激活值a越大,这条边权重的影响力就越大
梯度下降时候,并不只看每个参数是该增大还是减小,还看哪个参数的性价比最高
再看第三条路,改变上一层激活值,$w$为正时候,$a$越大越好,$w$为负时候$a$越小越好,和增加权重类似,改变上一层激活值,要依据对应权重大小,对激活值做出成比例的改变
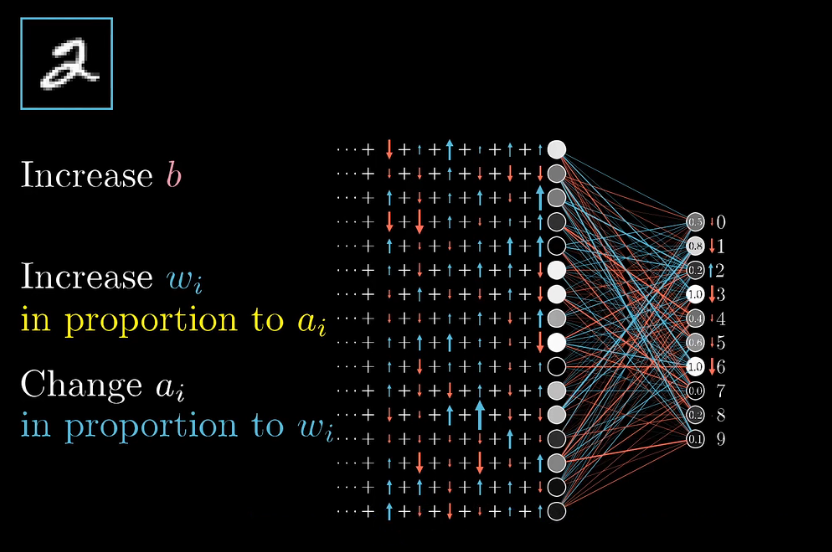
跳出2的神经元,从全局上看,我们还需要输出层其他神经元的激活值变弱,但输出层的每个神经元,对于如何改变倒数第二层都有各自的想法,所以我们会把2的神经元的期待,和别的输出神经元的期待全部加起来,作为如何改变倒数第二次神经元的指示。
这些期待变化不仅是对应的权重的倍数,也是每个神经元激活值改变量的倍数,这其实就是在实现反向传播的理念了。
把所有期待值加起来,就得到了一串对倒数第二层改动的变化量,重复这个过程,改变影响倒数第二层神经元激活值的相关参数,把这个过程循环到第一层。
再放大局面,上面只是训练单个样本“2”的影响,还要对其他所有的训练样本,同样的过一遍反向传播
记录下每个样本想怎样修改权重和偏置,在对每个参数的修改取一个平均值,不严格地说,这就是代价函数的负梯度,至少是标量的倍数:
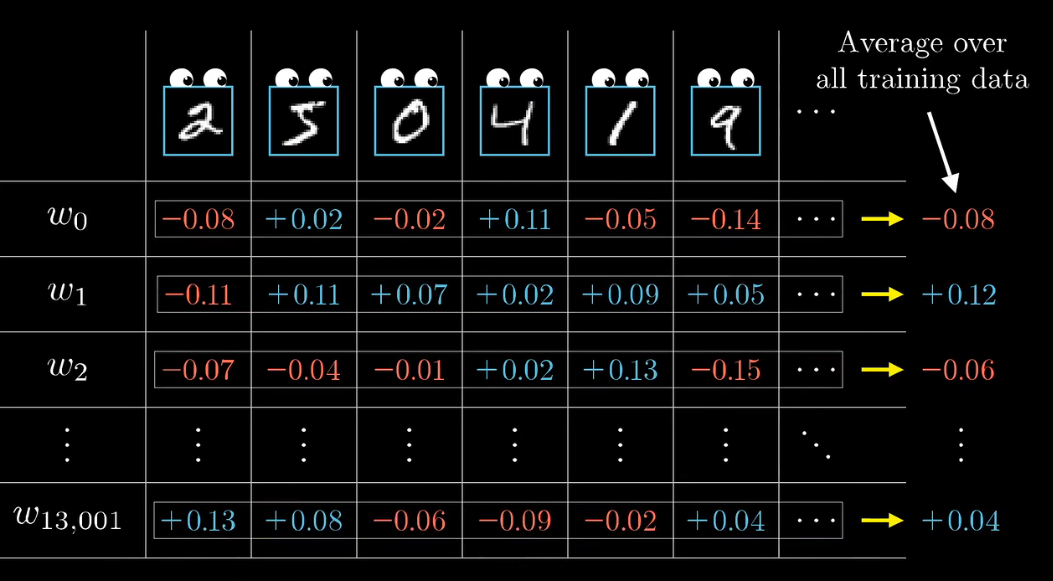
顺便在实际操作总,如果梯度下降的每一步,都用上每一个训练样本来计算的话,那么花的时间就太长了,所以一般把训练数据打乱,分成不同组,然后按组算出下降的一步。这不是代价函数真正的梯度,然而是个不错的近似,主要是计算量会降低不少。这个技巧叫做随机梯度下降 Stochastic gradient descent
微积分原理
反向传播最重要是对代价函数求导。
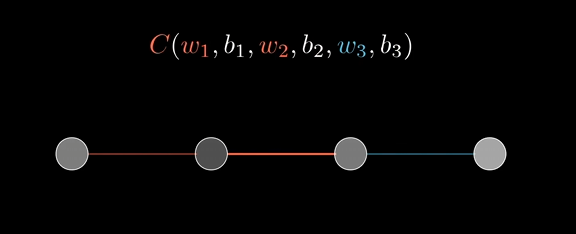
先考虑最简单的网络结构,每层只有一个神经元,只有三个权重和三个偏置。我们目标是找到代价函数对这些变量有多敏感,这样就能知道怎么调整代价降低最快。
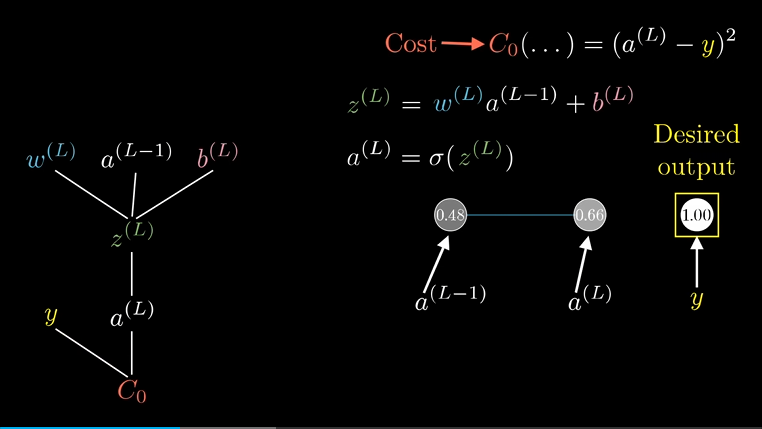
先关注最后两个神经元,激活值$a$的上标$L$表示它处在第$L$层,给定一个样本,把样本最终激活值要接近的目标叫做$y$。
这个网络对于单个训练样本的代价就是图上$C_0(…)$ ,把计算最后一层样本用到的加权和与偏置的和叫做$z^{(L)}$ ,当然最终的激活值$a^{(L)}$还经过了一个激活函数$\sigma(z^{(L)})$ 。
左边的树状结构展示了代价计算过程的层级先后,首我们拿权重、上层的激活值、偏置算出了$z$ ,然后通过激活函数算出了$a$ ,最后再结合$y$算出了代价$C_0$
我们的第一个目标是理解代价函数对权重$W^{(L)}$的微小变化有多敏感,也就是求$C$对于$w^{(L)}$的导数:
$$ \frac{\partial C}{\partial w^{(L)}} $$
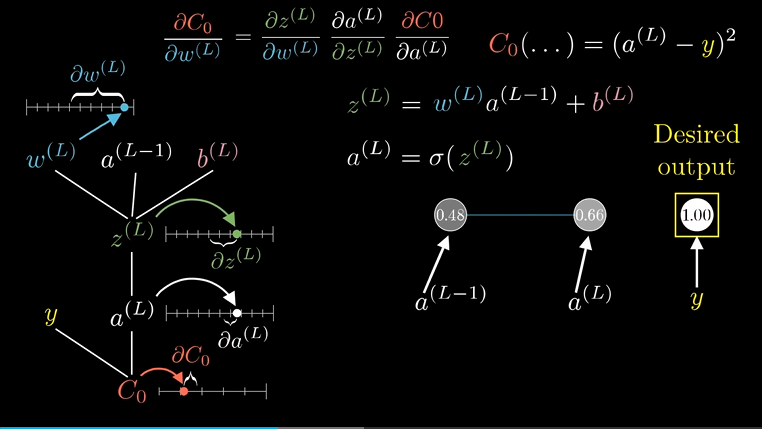
概念上来说$w^{(L)}$的微小变化,会导致$z(L)$产生变化,然后会导致$a^{(L)}$产生变化,最终影响到代价值。
可以根据链式法则,把三个比相乘,就可以算出$C$对$w^{(L)}$的微小变化有多敏感:
$$ \frac{\partial C_0}{\partial w^{(L)}} = \frac{\partial z^{L}}{\partial w^{(L)}} \frac{\partial a^{L}}{\partial z^{L}} \frac{\partial C_0}{\partial a^{L}} $$
一个个看:
$C_0$对$a^{(L)}$ 求导就是$2(a^{(L)}-y)$
$a^{(L)}$对$z^{(L)}$求导就是$\sigma ‘(z^{L})$ ,即对激活函数求导
$z^{(L)}$对$w^{(L)}$求导就是$a^{(L-1)}$ , 常量被干掉了,然后$w^{(L)}$一次方变零次方就是1,所以只剩上层激活值了
这只是一个样本,由于总的代价函数是许许多多训练样本所有代价的平均,它对$w^{(L)}$的导数就需要求这个表达式之于每一个训练样本的平均

当然这只是梯度向量$\nabla C$的一个分量:
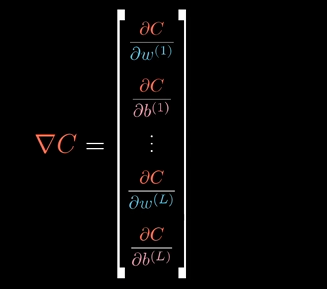
梯度向量$\nabla C$本身由代价函数对每一个权重和每一个偏置求偏导构成。对偏置求偏导步骤也基本相同,再树状结构上把$b^{(L)}$看作变量来求即可:
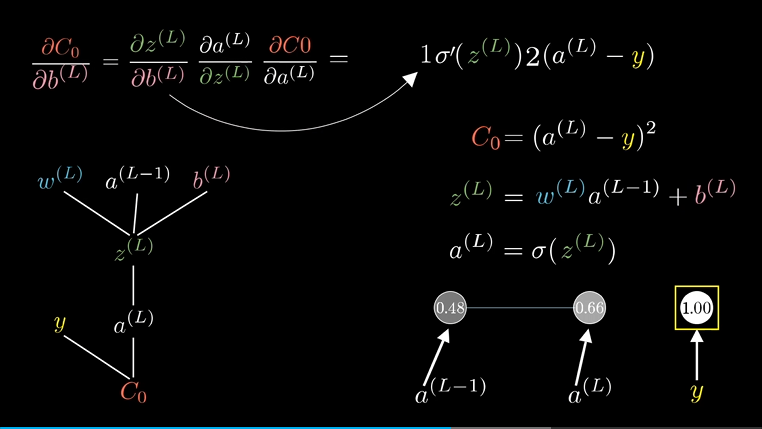
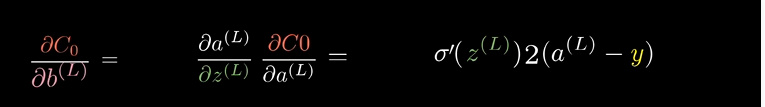
回到树的末梢,来看下这个代价函数对上一层的激活值$a^{(L-1)}$的敏感度,同样的计算思路:
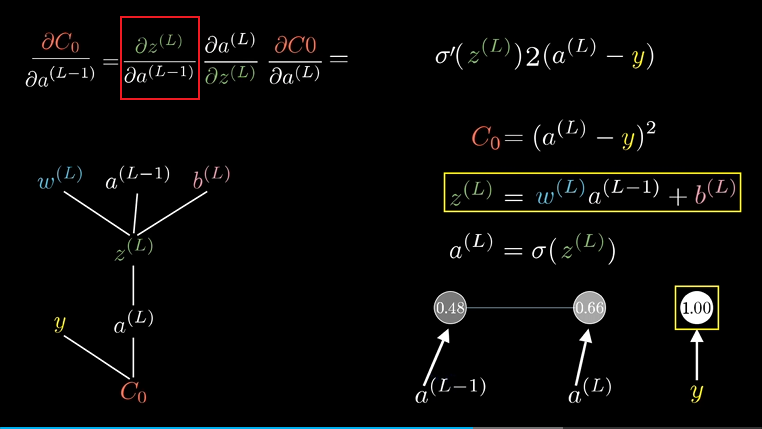
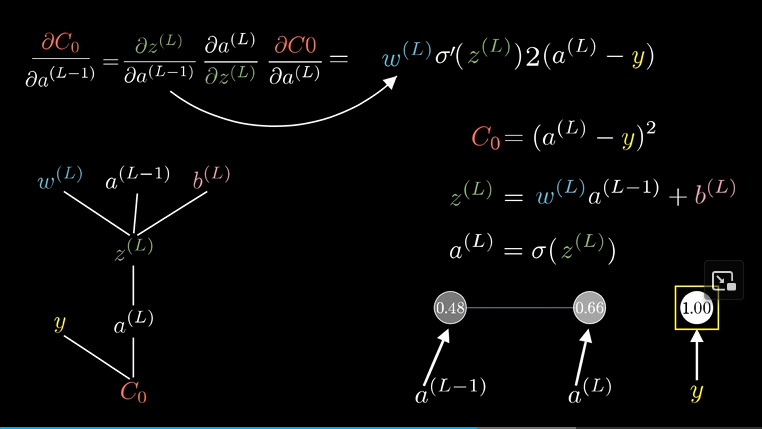
这样我们算出了代价函数对$(L-1)$层激活值的敏感度,虽说我们不能改变激活值,但我们仍然需要这个值,因为我们可以反向运用链式法则,来计算代价函数对之前的权重和偏置的敏感度。
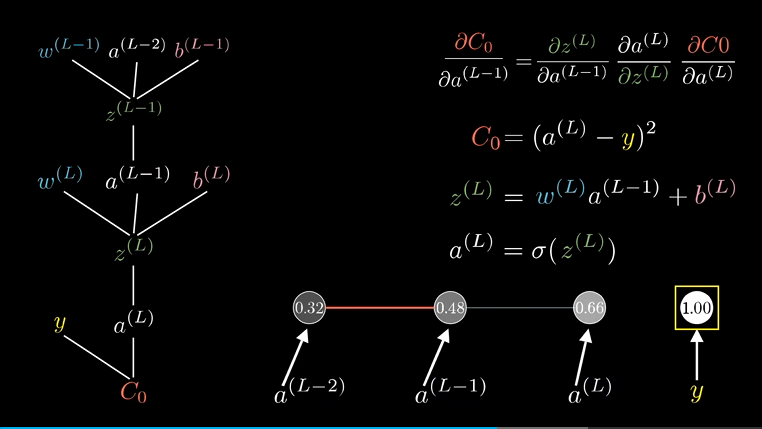
很显然,已经有$C_0$对$a^{(L-1)}$的导数的情况下,求更上面的节点的时候比如$w^{(L-1)}$,只要简单相乘就好了:
$$ \frac{\partial C_0}{\partial w^{(L-1)}} = \frac{\partial z^{(L-1)}}{\partial w^{(L-1)}} \frac{\partial a^{(L-1)}}{\partial z^{(L-1)}} \frac{\partial C_0}{\partial a^{(L-1)}} $$
妙蛙~
对于复杂的结构,无非是夺标几个下标,下标是神经元在当前层的节点编号:
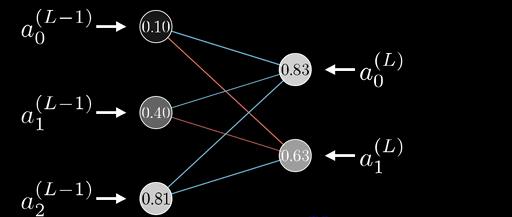
只是看着复杂,和每层只有一个神经元本质是一样的:
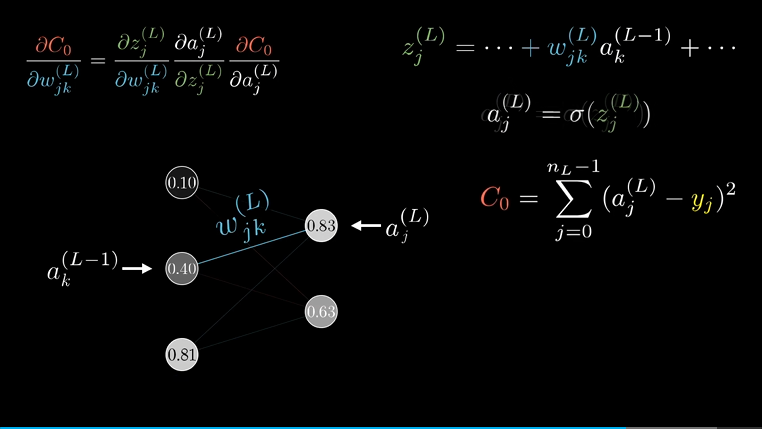
唯一改变的是,代价对$(L-1)$层激活值的导数,需要SUM,因为它有多条出边,如图上它同时影响$a^{(L)}_0$ 和$a^{(L)}_1$ 进而影响激活函数,所以得把它们加起来。
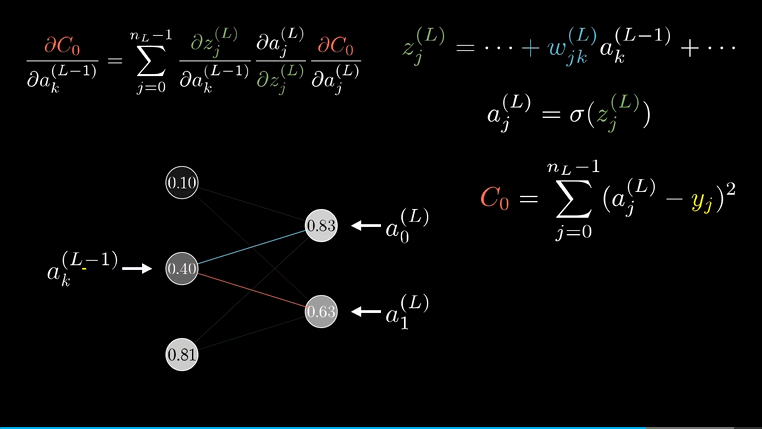
这样就完成了,只要算出来倒数第二层 代价函数对激活值的敏感度,接下来只要重复这个过程,计算喂给倒数第二层的权重和偏置就好了。这就是反向传播。
链式法则表达式给出了决定梯度每个分量的偏导,使得我们能够不断下探,最小化神经网络的代价。
ps:怎么更新,$w = w - 学习率 \times 偏导值$ ,学习率是梯度下降的步长
补充
激活函数:
早先都是使用Sigmoid映射加权值,后来发现ReLU(Rectified linear unit) 线性整流函数效果更好
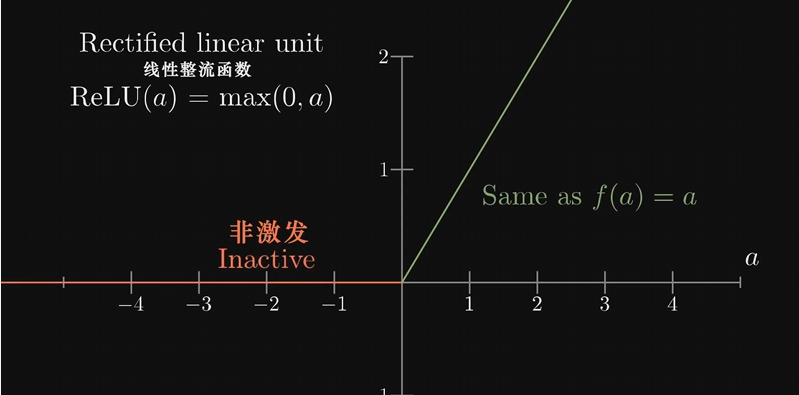
疑问:ReLU好像并不能让激活值在0到1之间?
训练数据:
MNIST数据库有搜集数以万计的手写数字图像